合作客戶/
拜耳公司 |
同濟(jì)大學(xué) |
聯(lián)合大學(xué) |
美國保潔 |
美國強(qiáng)生 |
瑞士羅氏 |
相關(guān)新聞Info
-
> 單片機(jī)智能控制的液體表面張力測量儀設(shè)計(jì)
> 毛細(xì)現(xiàn)象及潤濕作用機(jī)理相關(guān)解釋
> 不同溫度下手性離子液體及二元混合物的密度和表面張力(下)
> 表面張力儀的校準(zhǔn)方法
> 可視化實(shí)驗(yàn)方法研究電場作用下液滴撞擊表面的動(dòng)態(tài)行為(三)
> 混合型生物洗油菌發(fā)酵上清液的表面張力值測定(一)
> 多頻超聲波技術(shù)&人工神經(jīng)網(wǎng)絡(luò)構(gòu)建變壓器油界面張力預(yù)測模型(一)
> 植物油中N-酰基氨基酸表面活性劑的界面活性和聚集行為——摘要、簡介
> 打破試劑溶液的表面張力,提升乳糖醇制備的攪拌混合效果
> 界面張力在10-1mN/m的陰離子表面活性劑配比與性能測試
推薦新聞Info
-
> 影響?yīng)M縫間氫鍵流體氣液平衡界面張力的因素有哪些(三)
> 影響?yīng)M縫間氫鍵流體氣液平衡界面張力的因素有哪些(二)
> 影響?yīng)M縫間氫鍵流體氣液平衡界面張力的因素有哪些(一)
> GA、WPI和T80復(fù)合乳液體系的脂肪消化動(dòng)力學(xué)曲線、界面張力變化(四)
> GA、WPI和T80復(fù)合乳液體系的脂肪消化動(dòng)力學(xué)曲線、界面張力變化(三)
> GA、WPI和T80復(fù)合乳液體系的脂肪消化動(dòng)力學(xué)曲線、界面張力變化(二)
> GA、WPI和T80復(fù)合乳液體系的脂肪消化動(dòng)力學(xué)曲線、界面張力變化(一)
> 表面張力實(shí)驗(yàn)、接觸角實(shí)驗(yàn)分析抑塵試劑對煤的潤濕結(jié)果
> Kibron表面張力儀研究燒結(jié)礦聚結(jié)行為
> 基于界面張力和表面張力測試評(píng)估商用UV油墨對不同承印紙張的表面浸潤性差異(三)
接觸角遲滯時(shí)氣~液界面張力的溫度敏感性對液滴蒸發(fā)過程的影響——理論模型及計(jì)算方法
來源:物理學(xué)報(bào) 瀏覽 578 次 發(fā)布時(shí)間:2024-12-31
2理論模型及計(jì)算方法
2.1理論模型
假設(shè)一不可壓縮液滴在均勻加熱的固體表面上不斷蒸發(fā),如圖1所示,液滴初始最大厚度為,流動(dòng)方向尺度為L,壁面溫度為w.由于ε=?1(圖1中的H?,L?僅為表示清楚,不代表真實(shí)比例),因此可應(yīng)用潤滑理論(上標(biāo)~表示有量綱量,下同).
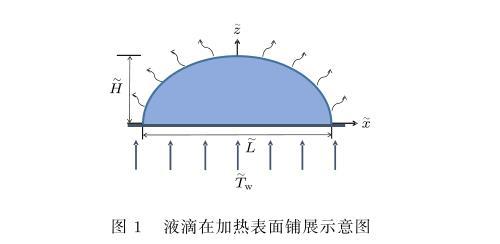
圖1液滴在加熱表面鋪展示意圖




液滴運(yùn)動(dòng)過程的控制方程包括連續(xù)性方程、動(dòng)量方程和能量方程:
界面處的蒸發(fā)流量與界面溫度有關(guān),可表示為
為避免接觸線處出現(xiàn)應(yīng)力奇點(diǎn),在水平方向施加Navier滑移邊界條件:
壁面溫度滿足
由于固-液、固-氣界面張力目前仍難以通過實(shí)驗(yàn)直接測量,假設(shè)固-液、固-氣界面張力不隨溫度改變,而氣-液界面張力與溫度滿足線性關(guān)系:
將控制方程和邊界條件采用下式進(jìn)行無量綱化:
通過無量綱變換和保留數(shù)量級(jí)≥Ο(ε),可得無量綱控制方程組為
無量綱邊界條件為無量綱形式的界面張力與溫度關(guān)系為
液滴表面溫度為
采用積分法可得液滴厚度的演化方程為
(27)式右側(cè)依次代表毛細(xì)力、重力、熱毛細(xì)力和蒸發(fā)在液滴運(yùn)動(dòng)過程中的作用.
液滴在理想光滑表面上,在三相接觸線處,Young方程為
為描述接觸角遲滯影響,采用以下線性經(jīng)驗(yàn)關(guān)聯(lián)式描述前進(jìn)接觸角和后退接觸角與遲滯角之間的關(guān)系:
式中,A≥0是與粗糙度無關(guān),與液體性質(zhì)有關(guān)的常數(shù);遲滯角Δθ與表面粗糙度和化學(xué)異質(zhì)性有關(guān).
接觸線處的液滴高度為零,即h(x=xcl=xcr,t)=0,其中xcl和xcr分別代表左側(cè)和右側(cè)接觸線位置.采用下式描述接觸線移動(dòng)速率與接觸角間的關(guān)系[28](下標(biāo)c代表接觸線):
式中,B和m為常數(shù);θ為動(dòng)態(tài)接觸角;υc>0代表接觸線向外鋪展,υc<0代表向內(nèi)收縮.
計(jì)算初始條件為
式中,F(x)=0.5[1+tanh(20x)].
基于Karapetsas等提出的坐標(biāo)變換法,將瞬態(tài)物理域(x,t)映射到固定計(jì)算域(x',t'),
液滴運(yùn)動(dòng)區(qū)域設(shè)定為–1≤x'≤1,時(shí)間導(dǎo)數(shù)表示如下:
(36)式用于替換控制方程(27)的相應(yīng)項(xiàng).
數(shù)值求解采用Freefem++14.3,該軟件是求解偏微分方程的強(qiáng)大工具,是一款免費(fèi)的、開放源代碼的有限元計(jì)算軟件,目前已經(jīng)比較成熟地運(yùn)用在各類數(shù)值模擬中,對于液滴、液膜的流體數(shù)值計(jì)算也很常見.該軟件采用Delaunay算法生成離散偏微分方程所需網(wǎng)格,具有網(wǎng)格自適應(yīng)和移動(dòng)網(wǎng)格生成的功能;采用稀疏矩陣存儲(chǔ)格式,內(nèi)存需求少,計(jì)算速度快,是求解復(fù)雜區(qū)域問題的高效計(jì)算軟件.
2.2計(jì)算模型驗(yàn)證
參照朱仙仙等用4μL去離子水在加熱溫度為60°的玻璃表面上的蒸發(fā)實(shí)驗(yàn)數(shù)據(jù),換算得到無量綱參數(shù),各參數(shù)取值為:ε=0.1,A=0.39,B=0.007,m=3,C=–0.004,Bo=0.007,Ca=0.5,K=10,E=1×10-3,Ωlg=0.003.首先,為了驗(yàn)證數(shù)值模擬結(jié)果的準(zhǔn)確性,將接觸角和接觸線隨時(shí)間變化的實(shí)驗(yàn)結(jié)果無量綱化后與模擬值進(jìn)行對比,結(jié)果如圖2(a)和圖2(b)所示.可以看出,Δθ=0.27時(shí)的模擬值與實(shí)驗(yàn)結(jié)果總體符合良好,即采用考慮接觸角遲滯的理論模型可更準(zhǔn)確地反映液滴的運(yùn)動(dòng)過程.值得注意的是,朱仙仙等所給實(shí)驗(yàn)結(jié)果并未呈現(xiàn)液滴鋪展階段,可能是由此階段變化較快、不易觀測記錄所致;模擬結(jié)果和實(shí)驗(yàn)結(jié)果有偏差的原因可能是實(shí)驗(yàn)時(shí)基底加熱時(shí)受熱不均勻或者基底傳熱能力不一致,也有可能是基于潤滑理論建立模型時(shí),未考慮液滴蒸氣擴(kuò)散所致.

圖2計(jì)算模型的驗(yàn)證(a)接觸角的演化過程;(b)接觸線的演化過程;(c)網(wǎng)格無關(guān)性驗(yàn)證
此外,模擬時(shí)進(jìn)行了網(wǎng)格無關(guān)性驗(yàn)證,在x方向上對比了網(wǎng)格數(shù)為300,500和800的結(jié)果,發(fā)現(xiàn)增加網(wǎng)格數(shù)使計(jì)算時(shí)長增大,而各特征參數(shù)計(jì)算結(jié)果數(shù)值差距不大,以圖2(c)的接觸線演化過程為例,網(wǎng)格數(shù)為500時(shí)可同時(shí)滿足精確性與高效性的要求.因此,計(jì)算中時(shí)間步長設(shè)為10–6,將[0,2]×[0,1]的計(jì)算域劃分為500×2個(gè)均勻網(wǎng)格.因方程(27)是一維的,液滴厚度h與y方向無關(guān),所以為節(jié)約計(jì)算時(shí)間,在y方向僅劃分2層網(wǎng)格.










